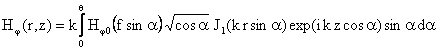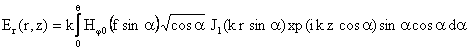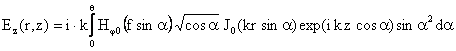Лазерные пучки с осесимметричным состоянием поляризации

Эллипсометрические параметры, характеризующие состояние поляризации в выбранной точке поперечного сечения луча:

• Отношение длин осей эллипса (a/b);
• Ориентация эллипса θ в выбранных координатах;
• Направление вращения вектора поля;
• Фаза φ в заданный момент времени.

Лазерные пучки с осесимметричным состоянием поляризации

Лазерные моды с радиальной и азимутальной поляризацией обладают уникальными свойствами и находят все большее применение в научных исследованиях и прикладных задачах. Основные достижения сотрудников ИПЛИТ РАН в этой области:

• Дано физически и математически корректное теоретическое описание.
• Разработан метод их генерации на основе интерферометра Саньяка для маломощных лазеров.
• Осуществлена генерация мод с R и A поляризацией в мощном СО₂ лазере с помощью дифракционных зеркал и аксиконов.
• Теоретически рекомендовано использование этих мод в лазерной обработке материалов.
• Показана эффективность использования таких мод в качестве ловушек для холодных атомов.
• Разработан поляризационный микрозонд для диагностики биомолекул.
• Проведены расчеты по поглощению такого излучения при лазерном нагреве плазмы, и по ускорению релятивистских электронов в продольном поле.

Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности лазерной резки металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия.

Выходное излучение большинства современных лазеров является поляризационно-однородным. В этом случае эллипсометрические параметры излучения во всех точках поперечного сечения лазерного пучка одинаковы. Распределение амплитуды поля в поперечном сечении луча (поперечные моды) при однородной поляризации описывается решением скалярного волнового уравнения. Для круглых зеркал это Лагерр – Гауссовы моды. Среди решений векторного волнового уравнения есть класс поляризационно-неоднородных мод (ПНМ). В этих модах один или несколько эллипсометрических параметров не являются постоянными по сечению луча. Например, радиально и азимутально поляризованные моды имеют линейную поляризацию в каждой точке, однако, направление поля различно в разных точках поперечного сечения луча. В другом случае от точки к точке изменяется тип поляризации: линейная, эллиптическая, круговая. Наибольший практический интерес представляют моды с радиальным и азимутальным направлением поляризации, имеющие аксиальную симметрию всех параметров лазерного луча, включая поляризацию Некоторые типы поляризационно-неоднородных мод. а – радиально поляризованная, б – угол между вектором поля и радиусом постоянен, в – азимутально поляризованная мода, г – линейная поляризация со сложной топологией вектора поля, д – изменение типа поляризации от точки к точке поперечного сечения луча.

Распределения поля в однородно поляризованных Лагерр – Гауссовых модах TEMpq. Пример направления поля в моде высокого порядка

Существуют два принципиальных способа получения осесимметрично-поляризованного излучения:

• Внутрирезонаторный, с использованием, например, дифракционных зеркал с высокой локальной поляризационной селективностью. Специальный рисунок рельефа обеспечивает максимальную добротность резонатора для заданной моды. При этом остальные моды подавляются, имея значительные внутрирезонаторные потери. Этот метод является предпочтительным для мощных лазеров.
• Внерезонаторные методы формирования ПНМ основаны на когерентной суперпозиции пары обычных мод с помощью интерферометра. Такая техника удобна для лазеров с малой длиной волны, низким коэффициентом усиления и высокой добротностью резонатора. Излучение таких лазеров обладает высоким качеством, имеет высокую пространственную и временную когерентность.

Теоретическое описание

Схема образование радиально и азимутально поляризованных мод как суперпозиция «обычных» мод ТЕМ₀₁.

Теоретическое описание радиально и азимутально поляризованных мод по этой схеме, с использованием классических решений для Лагерр-Гауссовых мод с однородной поляризацией, нерационально, поскольку классические решения имеют серьезные внутренние противоречия.

Представим магнитное поле в виде H=H_φ(r,z)e_φ(φ), тогда уравнение ∇H=0 удовлетворяется, а векторное волновое уравнение сводится к скалярному. Его решением в параксиальном приближении является r-z часть известного выражения для Лагерр-Гауссовых мод TEM_pq при q=1. Компоненты электрического поля E_r и E_z определяются через уравнение Максвелла . Для перетяжки, z=0, решения имеют вид:

Здесь R₀ = r/w₀ ,

Учитывая симметрию уравнений Максвелла таким образом можно вычислять компоненты полей для двух классов мод:

H=H_φ(r,z)•e_φ(φ), E=E_r(r,z)•e_r(φ) + E_z(r,z)e_z

E=E_φ(r,z)•e_φ(φ), H=H_r(r,z)•e_r(φ) + H_z(r,z)e_z

Ниже приведены выражения для компонент полей в перетяжке z0 для случая острой фокусировки, так называемое приближение Дебая.

Здесь θ - угол, определяемый апертурой пучка и фокусным расстоянием линзы f. Аналогичные формулы могут быть записаны и для компонент поля E_φ(r,z), H_r(r,z), H_z(r,z).