Лазерные пучки с осесимметричным состоянием поляризации

Эллипсометрические параметры, характеризующие состояние поляризации в выбранной точке поперечного сечения луча:

• Отношение длин осей эллипса (a/b);
• Ориентация эллипса θ в выбранных координатах;
• Направление вращения вектора поля;
• Фаза φ в заданный момент времени.

Лазерные пучки с осесимметричным состоянием поляризации

Лазерные моды с радиальной и азимутальной поляризацией обладают уникальными свойствами и находят все большее применение в научных исследованиях и прикладных задачах. Основные достижения сотрудников ИПЛИТ РАН в этой области:

• Дано физически и математически корректное теоретическое описание.
• Разработан метод их генерации на основе интерферометра Саньяка для маломощных лазеров.
• Осуществлена генерация мод с R и A поляризацией в мощном СО₂ лазере с помощью дифракционных зеркал и аксиконов.
• Теоретически рекомендовано использование этих мод в лазерной обработке материалов.
• Показана эффективность использования таких мод в качестве ловушек для холодных атомов.
• Разработан поляризационный микрозонд для диагностики биомолекул.
• Проведены расчеты по поглощению такого излучения при лазерном нагреве плазмы,

и по ускорении релятивистских электронов в продольном поле.

Распределения поля в однородно поляризованных Лагерр – Гауссовых модах TEM_pq.

Пример направления поля в моде высокого порядка

Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности лазерной резки металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия.

Выходное излучение большинства современных лазеров является поляризационно-однородным. В этом случае эллипсометрические параметры излучения во всех точках поперечного сечения лазерного пучка одинаковы.

Распределение амплитуды поля в поперечном сечении луча (поперечные моды) при однородной поляризации описывается решением скалярного волнового уравнения. Для круглых зеркал это Лагерр – Гауссовы моды.

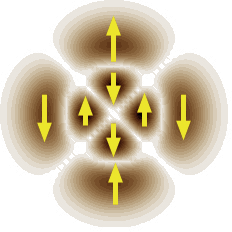
Среди решений векторного волнового уравнения есть класс поляризационно-неоднородных мод (ПНМ). В этих модах один или несколько эллипсометрических параметров не являются постоянными по сечению луча. Например, радиально и азимутально поляризованные моды имеют линейную поляризацию в каждой точке, однако, направление поля различно в разных точках поперечного сечения луча. В другом случае от точки к точке изменяется тип поляризации: линейная, эллиптическая, круговая.

Наибольший практический интерес представляют моды с радиальным и азимутальным направлением поляризации, имеющие аксиальную симметрию всех параметров лазерного луча, включая поляризацию

Некоторые типы поляризационно-неоднородных мод.
а – радиально поляризованная, б – угол между вектором поля и радиусом постоянен, в – азимутально поляризованная мода, г – линейная поляризация со сложной топологией вектора поля, д – изменение типа поляризации от точки к точке поперечного сечения луча.