Лазерные пучки с осесимметричным состоянием поляризации — различия между версиями
EvgBot (обсуждение | вклад) м |
EvgBot (обсуждение | вклад) м |
||
| Строка 16: | Строка 16: | ||
* Показана эффективность использования таких мод в качестве ловушек для холодных атомов. | * Показана эффективность использования таких мод в качестве ловушек для холодных атомов. | ||
* Разработан поляризационный микрозонд для диагностики биомолекул. | * Разработан поляризационный микрозонд для диагностики биомолекул. | ||
| − | * Проведены расчеты по поглощению такого излучения при лазерном нагреве [[плазма|плазмы]], | + | * Проведены расчеты по поглощению такого излучения при лазерном нагреве [[плазма|плазмы]], и по ускорению релятивистских электронов в продольном поле. |
| − | и по | + | |
| − | |||
| − | |||
Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности [[Лазерная резка|лазерной резки]] металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия. | Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности [[Лазерная резка|лазерной резки]] металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия. | ||
| + | {| border=0 | ||
| + | | | ||
Выходное излучение большинства современных лазеров является поляризационно-однородным. В этом случае эллипсометрические параметры излучения во всех точках поперечного сечения лазерного пучка одинаковы. | Выходное излучение большинства современных лазеров является поляризационно-однородным. В этом случае эллипсометрические параметры излучения во всех точках поперечного сечения лазерного пучка одинаковы. | ||
| Строка 31: | Строка 30: | ||
Наибольший практический интерес представляют моды с радиальным и азимутальным направлением поляризации, имеющие аксиальную симметрию всех параметров лазерного луча, включая поляризацию | Наибольший практический интерес представляют моды с радиальным и азимутальным направлением поляризации, имеющие аксиальную симметрию всех параметров лазерного луча, включая поляризацию | ||
| − | [[Файл:Лазерные пучки Image011.gif|thumb| | + | [[Файл:Лазерные пучки Image011.gif|thumb|500px|center|Некоторые типы поляризационно-неоднородных мод. <br />а – радиально поляризованная, б – угол между вектором поля и радиусом постоянен, в – азимутально поляризованная мода, г – линейная поляризация со сложной топологией вектора поля, д – изменение типа поляризации от точки к точке поперечного сечения луча.]] |
| + | |||
| + | | | ||
| + | [[Файл:Лазерные пучки Image006.png|thumb|240px|Распределения поля в однородно поляризованных Лагерр – Гауссовых модах TEM<sub>pq</sub>.]] | ||
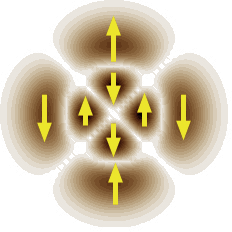
| + | [[Файл:Лазерные пучки Image008.png|thumb|240px|Пример направления поля в моде высокого порядка]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | Существуют два принципиальных способа получения осесимметрично-поляризованного излучения: | ||
| + | |||
| + | * '''Внутрирезонаторный''', с использованием, например, дифракционных зеркал с высокой локальной поляризационной селективностью. Специальный рисунок рельефа обеспечивает максимальную добротность резонатора для заданной моды. При этом остальные моды подавляются, имея значительные внутрирезонаторные потери. Этот метод является предпочтительным для мощных лазеров. | ||
| + | * '''Внерезонаторны'''е методы формирования ПНМ основаны на когерентной суперпозиции пары обычных мод с помощью [[интерферометр]]а. Такая техника удобна для лазеров с малой длиной волны, низким коэффициентом усиления и высокой добротностью резонатора. Излучение таких лазеров обладает высоким качеством, имеет высокую пространственную и временную когерентность. | ||
| + | |||
| + | == Теоретическое описание == | ||
| + | |||
| + | Теоретическое описание радиально и азимутально поляризованных мод по этой схеме, с использованием классических решений для Лагерр-Гауссовых мод с однородной поляризацией, нерационально, поскольку классические решения имеют серьезные внутренние противоречия. | ||
| + | Представим магнитное поле в виде '''H'''=H<sub>φ</sub>(r,z)'''e'''<sub>φ</sub>(φ), тогда уравнение ∇'''H'''=0 удовлетворяется, а векторное волновое уравнение сводится к скалярному. Его решением в параксиальном приближении является r-z часть известного выражения для Лагерр-Гауссовых мод TEM<sub>pq</sub> при q=1. Компоненты электрического поля E<sub>r</sub> и E<sub>z</sub> определяются через уравнение [[Максвелл]]а [[Файл:Лазерные пучки Image015.gif]]. Для перетяжки, z=0, решения имеют вид: | ||
| + | [[Файл:Лазерные пучки Image017.gif|center]] | ||
| + | [[Файл:Лазерные пучки Image019.gif|center]] | ||
| + | |||
| + | Здесь R<sub>0</sub> = r/w<sub>0</sub> , [[Файл:Лазерные пучки Image021.gif]] | ||
| + | |||
| + | Учитывая симметрию уравнений Максвелла таким образом можно вычислять компоненты полей для двух классов мод: | ||
| + | :'''H'''=H<sub>φ</sub>(r,z)•'''e'''<sub>φ</sub>(φ), '''E'''=E<sub>r</sub>(r,z)•'''e'''<sub>r</sub>(φ) + E<sub>z</sub>(r,z)'''e'''<sub>z</sub> | ||
| + | :'''E'''=E<sub>φ</sub>(r,z)•'''e'''<sub>φ</sub>(φ), '''H'''=H<sub>r</sub>(r,z)•'''e'''<sub>r</sub>(φ) + H<sub>z</sub>(r,z)'''e'''<sub>z</sub> | ||
[[Категория:Поляризация]] | [[Категория:Поляризация]] | ||
[[Категория:Лазеры]] | [[Категория:Лазеры]] | ||
Версия 00:55, 27 марта 2009
Лазерные пучки с осесимметричным состоянием поляризации
Лазерные моды с радиальной и азимутальной поляризацией обладают уникальными свойствами и находят все большее применение в научных исследованиях и прикладных задачах. Основные достижения сотрудников ИПЛИТ РАН в этой области:
- Дано физически и математически корректное теоретическое описание.
- Разработан метод их генерации на основе интерферометра Саньяка для маломощных лазеров.
- Осуществлена генерация мод с R и A поляризацией в мощном СО2 лазере с помощью дифракционных зеркал и аксиконов.
- Теоретически рекомендовано использование этих мод в лазерной обработке материалов.
- Показана эффективность использования таких мод в качестве ловушек для холодных атомов.
- Разработан поляризационный микрозонд для диагностики биомолекул.
- Проведены расчеты по поглощению такого излучения при лазерном нагреве плазмы, и по ускорению релятивистских электронов в продольном поле.
Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности лазерной резки металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия.
Существуют два принципиальных способа получения осесимметрично-поляризованного излучения:
- Внутрирезонаторный, с использованием, например, дифракционных зеркал с высокой локальной поляризационной селективностью. Специальный рисунок рельефа обеспечивает максимальную добротность резонатора для заданной моды. При этом остальные моды подавляются, имея значительные внутрирезонаторные потери. Этот метод является предпочтительным для мощных лазеров.
- Внерезонаторные методы формирования ПНМ основаны на когерентной суперпозиции пары обычных мод с помощью интерферометра. Такая техника удобна для лазеров с малой длиной волны, низким коэффициентом усиления и высокой добротностью резонатора. Излучение таких лазеров обладает высоким качеством, имеет высокую пространственную и временную когерентность.
Теоретическое описание
Теоретическое описание радиально и азимутально поляризованных мод по этой схеме, с использованием классических решений для Лагерр-Гауссовых мод с однородной поляризацией, нерационально, поскольку классические решения имеют серьезные внутренние противоречия.
Представим магнитное поле в виде H=Hφ(r,z)eφ(φ), тогда уравнение ∇H=0 удовлетворяется, а векторное волновое уравнение сводится к скалярному. Его решением в параксиальном приближении является r-z часть известного выражения для Лагерр-Гауссовых мод TEMpq при q=1. Компоненты электрического поля Er и Ez определяются через уравнение Максвелла ![]() . Для перетяжки, z=0, решения имеют вид:
. Для перетяжки, z=0, решения имеют вид:
Учитывая симметрию уравнений Максвелла таким образом можно вычислять компоненты полей для двух классов мод:
- H=Hφ(r,z)•eφ(φ), E=Er(r,z)•er(φ) + Ez(r,z)ez
- E=Eφ(r,z)•eφ(φ), H=Hr(r,z)•er(φ) + Hz(r,z)ez